| PARAMÈTRES EXPÉRIMENTAUX | |
| Longueur d'onde : | λ = ... |
| Écartement des sources : | a = ... |
| Distance sources-écran : | D = ... |
| PARAMÈTRES CALCULÉS | |
| Différence de marche : | δ = S2M - S1M = ... |
| Interfrange : | i = λD/a = ... |
| Ordre d'interférences : | p = δ/λ = ... |
SIMULATION D'INTERFÉRENCES LUMINEUSES
Version 1.3.2 du 09/09/2025
Thomas ROY
thomas.roy@outlook.com
La dernière version est téléchargeable sur physique-pcsi.prepa-balzac.fr.
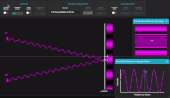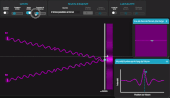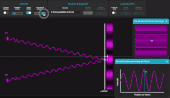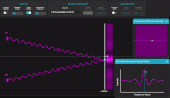
Fentes d'Young (les bases…)
Sélectionner les sources « 2 fentes parallèles à l'écran », et afficher la fenêtre « Signal ». Modifier l'écartement a des sources et la distance D sources-écran pour observer l'influence sur l'interfrange i=λD/A. Activer l'interrupteur « Signal » et déplacer le point le long de l'écran pour constater que les rayons arrivent en phase sur une frange claire et en opposition de phase sur une frange sombre (on peut mettre l'animation en pause pour le constater plus aisément).
En CPGE 1re année, on peut aussi montrer en activant l'interrupteur « Ecran large » que loin de l'axe optique, l'interfrange n'est plus constante car l'approximation n'est plus valable.

Perte de contraste avec une source étendue
En mode « Source étendue », augmenter la largeur de la fente source devant les fentes d'Young pour constater la perte de contraste. Pour l'expliquer, déplacer le point P sur la fente source : la bande étroite située juste derrière l'écran montre la figure d'interférences si ce point P était seul. La figure d'interférences totale observée à l'écran est la superposition des figures générées par chaque point P de la source étendue.

3 fentes (ou plus) : maxima secondaires
En passant au mode « N fentes », affichez le graphe de l'intensité relative le long de l'écran, et en modifiant le nombre de fentes montrez l'existence de maxima secondaires. En augmentant encore le nombre de fentes, on s'approche d'un réseau de diffraction où l'on obtient différents ordres discrets, directions dans lesquelles un rayon lumineux est diffracté.

Effets d'une lame de verre : longueur d'onde modifiée, défilement des franges
En plaçant une lame de verre, modifier l'épaisseur e de la lame et/ou l'indice n du verre pour constater le défilement des franges. On remarque que la longueur d'onde λ = λ0/n est modifiée dans le verre lorsque l'on fait varier l'indice n.

Hyperboloïdes dans l'espace / Passage du Michelson « coin d'air » à « lame d'air »
Montrez le champ d'interférences partout dans l'espace généré par deux sources ponctuelles, générant ainsi des hyperboloïdes de révolution, en sélectionnant les sources « 2 points libres » (les deux sources ponctuelles sont ainsi déplaçables librement), et activez l'affichage « Champ partout ». Déplacez ensuite les deux sources à la souris.

Explication du spectre cannelé en lumière blanche
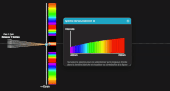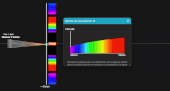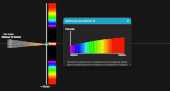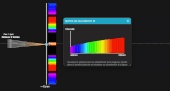
En mode lumière blanche, on peut expliquer le spectre cannelé en déplaçant le point M sur l'écran puis en balayant à la souris le spectre de la lumière reçue au niveau de ce point M. Sur la fenêtre principale de l'application s'affiche alors la figure d'interférence si cette longueur d'onde était émise seule. Le spectre cannelé observé résulte alors du mélange de toutes les couleurs, en chaque point M.

Miroir de Lloyd : déphasage de π à la réflexion
Sélectionner « Miroir de Lloyd » dans le menu déroulant « Sources », et déplacer le point M le long de l'écran. On constate le déphasage de π à la réflexion sur le miroir. La source virtuelle S' est l'image de la source ponctuelle S par le miroir (source S que l'on peut également déplacer).

Plusieurs spectres avec un réseau en lumière blanche
Passez en mode "N fentes" et activez la source de lumière blanche. Faites varier le nombre de fentes pour obtenir un réseau plus ou moins diffractant, et observez les différents ordres. En survolant le spectre à la souris, constatez qu'à l'ordre 0, toutes les longueurs d'onde arrivent au point O sur l'écran, d'où une raie blanche.
Notion de cohérence
Avec une lumière monochromatique et deux fentes sources, activez l'interrupteur "Train d'ondes", et constatez la perte de contraste en diminuant la longueur de cohérence. Observez les sauts de phase plus fréquents, en affichant les rayons en mode "sinusoïdes" (plus faciles à repérer qu'en mode "droites).